简介
在目标检测任务中，分类和检测框的回归是核心问题，损失函数的选择对模型的表现效果具有较大影响，本文介绍常用的损失函数 IoU、GIoU、DIou 和 CIoU。
IoU
IoU 是使用最广泛的检测框损失函数，大部分的检测算法都是使用的这个方法。IoU 也就是交并比(Intersection over Union)，预测框和真实框相交区域面积和合并区域面积的比值，计算公式如下
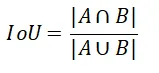
IoU 的代码实现
import numpy as np
def Iou(box1, box2, wh=False):
if wh == False:
xmin1, ymin1, xmax1, ymax1 = box1
xmin2, ymin2, xmax2, ymax2 = box2
else:
xmin1, ymin1 = int(box1[0]-box1[2]/2.0), int(box1[1]-box1[3]/2.0)
xmax1, ymax1 = int(box1[0]+box1[2]/2.0), int(box1[1]+box1[3]/2.0)
xmin2, ymin2 = int(box2[0]-box2[2]/2.0), int(box2[1]-box2[3]/2.0)
xmax2, ymax2 = int(box2[0]+box2[2]/2.0), int(box2[1]+box2[3]/2.0)
# 获取矩形框交集对应的左上角和右下角的坐标
xx1 = np.max([xmin1, xmin2])
yy1 = np.max([ymin1, ymin2])
xx2 = np.min([xmax1, xmax2])
yy2 = np.min([ymax1, ymax2])
# 计算两个矩形框面积
area1 = (xmax1-xmin1) * (ymax1-ymin1)
area2 = (xmax2-xmin2) * (ymax2-ymin2)
# 计算交集面积
inter_area = (np.max([0, xx2-xx1])) * (np.max([0, yy2-yy1]))
# 计算交并比
iou = inter_area / (area1+area2-inter_area+1e-6)
return iouIoU 的缺点：
如果两个框没有重叠，那么 IoU 等于0，这时候就没有梯度的回传，就无法进行学习训练
GIoU
2019年 CVPR，GIoU 在论文 Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression 中被提出
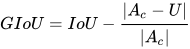
上述公式的含义：先计算两个框的最小闭包区域面积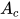 
(也同时包含了预测框和真实框的最小框的面积)，再计算闭包区域中不属于两个框的区域占闭包区域的比重，最后用 IoU 减去这个比重就得到 GIoU。
GIoU 的代码实现
def Giou(rec1,rec2):
# 分别是第一个矩形左右上下的坐标
x1,x2,y1,y2 = rec1
x3,x4,y3,y4 = rec2
iou = Iou(rec1,rec2)
area_C = (max(x1,x2,x3,x4)-min(x1,x2,x3,x4))*(max(y1,y2,y3,y4)-min(y1,y2,y3,y4))
area_1 = (x2-x1)*(y1-y2)
area_2 = (x4-x3)*(y3-y4)
sum_area = area_1 + area_2
# 第一个矩形的宽
w1 = x2 - x1
# 第二个矩形的宽
w2 = x4 - x3
h1 = y1 - y2
h2 = y3 - y4
# 交叉部分的宽
W = min(x1,x2,x3,x4)+w1+w2-max(x1,x2,x3,x4)
# 交叉部分的高
H = min(y1,y2,y3,y4)+h1+h2-max(y1,y2,y3,y4)
# 交叉的面积
Area = W*H
# 两矩形并集的面积
add_area = sum_area - Area
# 闭包区域中不属于两个框的区域占闭包区域的比重
end_area = (area_C - add_area)/area_C
giou = iou - end_area
return giouGIoU 考虑到了当检测框和真实框没有出现重叠的情况，但是当检测框和真实框之间出现包含的现象的时候 GIoU 就和 IoU 是同样的效果了。
DIoU
DIoU 即 Distance-IoU，计算公式如下
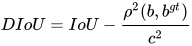
其中， b，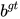 
分别代表了预测框和真实框的中心点，且 
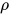代表的是计算两个中心点间的欧式距离。 c 代表的是能够同时包含预测框和真实框的最小闭包区域的对角线距离。
DIoU 考虑到 GIoU 的缺点，也是增加了两个框的最小闭包，将真实框和预测框都包含了进来，但是 DIoU 计算的不是框之间的交并，而是计算每个检测框之间的欧氏距离，这样就可以解决 GIoU 包含时出现的问题，同时，DIoU 最小化预测框间的中心点距离，从而能够达到快速收敛。
DIoU 代码实现
def Diou(bboxes1, bboxes2):
rows = bboxes1.shape[0]
cols = bboxes2.shape[0]
dious = torch.zeros((rows, cols))
if rows * cols == 0:#
return dious
exchange = False
if bboxes1.shape[0] > bboxes2.shape[0]:
bboxes1, bboxes2 = bboxes2, bboxes1
dious = torch.zeros((cols, rows))
exchange = True
# #xmin,ymin,xmax,ymax->[:,0],[:,1],[:,2],[:,3]
w1 = bboxes1[:, 2] - bboxes1[:, 0]
h1 = bboxes1[:, 3] - bboxes1[:, 1]
w2 = bboxes2[:, 2] - bboxes2[:, 0]
h2 = bboxes2[:, 3] - bboxes2[:, 1]
area1 = w1 * h1
area2 = w2 * h2
center_x1 = (bboxes1[:, 2] + bboxes1[:, 0]) / 2
center_y1 = (bboxes1[:, 3] + bboxes1[:, 1]) / 2
center_x2 = (bboxes2[:, 2] + bboxes2[:, 0]) / 2
center_y2 = (bboxes2[:, 3] + bboxes2[:, 1]) / 2
inter_max_xy = torch.min(bboxes1[:, 2:],bboxes2[:, 2:])
inter_min_xy = torch.max(bboxes1[:, :2],bboxes2[:, :2])
out_max_xy = torch.max(bboxes1[:, 2:],bboxes2[:, 2:])
out_min_xy = torch.min(bboxes1[:, :2],bboxes2[:, :2])
inter = torch.clamp((inter_max_xy - inter_min_xy), min=0)
inter_area = inter[:, 0] * inter[:, 1]
inter_diag = (center_x2 - center_x1)**2 + (center_y2 - center_y1)**2
outer = torch.clamp((out_max_xy - out_min_xy), min=0)
outer_diag = (outer[:, 0] ** 2) + (outer[:, 1] ** 2)
union = area1+area2-inter_area
dious = inter_area / union - (inter_diag) / outer_diag
dious = torch.clamp(dious,min=-1.0,max = 1.0)
if exchange:
dious = dious.T
return diousCIoU
CIoU 即 Complete-IoU，就是在 DIoU 的基础上增加了长和宽的损失，能够进一步地快速收敛和提升性能。
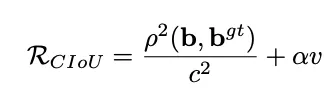
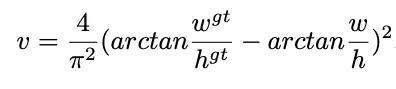
其中，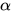
是权重函数，而 
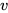用来度量长宽比的相似性
而完整的 CIoU 损失函数定位为
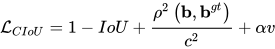
CIoU 的梯度类似于 DIoU，但还要考虑 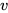的梯度，在长宽在[0, 1]的情况下，会导致梯度爆炸。
CIoU 代码实现
def bbox_overlaps_ciou(bboxes1, bboxes2):
rows = bboxes1.shape[0]
cols = bboxes2.shape[0]
cious = torch.zeros((rows, cols))
if rows * cols == 0:
return cious
exchange = False
if bboxes1.shape[0] > bboxes2.shape[0]:
bboxes1, bboxes2 = bboxes2, bboxes1
cious = torch.zeros((cols, rows))
exchange = True
w1 = bboxes1[:, 2] - bboxes1[:, 0]
h1 = bboxes1[:, 3] - bboxes1[:, 1]
w2 = bboxes2[:, 2] - bboxes2[:, 0]
h2 = bboxes2[:, 3] - bboxes2[:, 1]
area1 = w1 * h1
area2 = w2 * h2
center_x1 = (bboxes1[:, 2] + bboxes1[:, 0]) / 2
center_y1 = (bboxes1[:, 3] + bboxes1[:, 1]) / 2
center_x2 = (bboxes2[:, 2] + bboxes2[:, 0]) / 2
center_y2 = (bboxes2[:, 3] + bboxes2[:, 1]) / 2
inter_max_xy = torch.min(bboxes1[:, 2:],bboxes2[:, 2:])
inter_min_xy = torch.max(bboxes1[:, :2],bboxes2[:, :2])
out_max_xy = torch.max(bboxes1[:, 2:],bboxes2[:, 2:])
out_min_xy = torch.min(bboxes1[:, :2],bboxes2[:, :2])
inter = torch.clamp((inter_max_xy - inter_min_xy), min=0)
inter_area = inter[:, 0] * inter[:, 1]
inter_diag = (center_x2 - center_x1)**2 + (center_y2 - center_y1)**2
outer = torch.clamp((out_max_xy - out_min_xy), min=0)
outer_diag = (outer[:, 0] ** 2) + (outer[:, 1] ** 2)
union = area1+area2-inter_area
u = (inter_diag) / outer_diag
iou = inter_area / union
with torch.no_grad():
arctan = torch.atan(w2 / h2) - torch.atan(w1 / h1)
v = (4 / (math.pi ** 2)) * torch.pow((torch.atan(w2 / h2) - torch.atan(w1 / h1)), 2)
S = 1 - iou
alpha = v / (S + v)
w_temp = 2 * w1
ar = (8 / (math.pi ** 2)) * arctan * ((w1 - w_temp) * h1)
cious = iou - (u + alpha * ar)
cious = torch.clamp(cious,min=-1.0,max = 1.0)
if exchange:
cious = cious.T
return cious
