软硬件环境
- ubuntu 18.04 64bit
- anaconda with python 3.6
- numpy 1.12.1
前言
维基百科上给的定义
计程车几何(Taxicab geometry)或曼哈顿距离(Manhattan distance or Manhattan length)或方格线距离是由十九世纪的赫尔曼·闵可夫斯基所创辞汇,为欧几里得几何度量空间的几何学之用语,用以标明两个点上在标准坐标系上的绝对轴距之总和。
想象你在曼哈顿,要从一个十字路口开车到另外一个十字路口,实际驾驶距离就是这个“曼哈顿距离”。而这也是曼哈顿距离名称的来源,曼哈顿距离也称为城市街区距离。
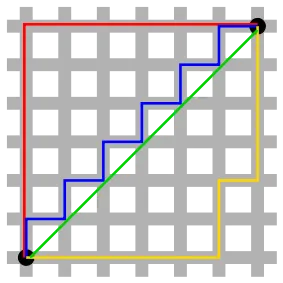
在上图中,绿线是欧几里得距离,红线是曼哈顿距离,蓝线和黄线是等价的曼哈顿距离。
二维平面两点a(x1,y1)与b(x2,y2)间的曼哈顿距离
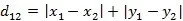
两个n维向量a(x11,x12,…,x1k)与 b(x21,x22,…,x2k)间的曼哈顿距离
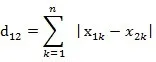
代码实现
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Date : 2018-08-20 16:10:23
# @Author : xugaoxiang (djstava@gmail.com)
# @Link : link
# @Version : 1.0.0
import os
import numpy as np
def get_manhattan_distance(vect1, vect2):
dist = np.sum(np.abs(vect1 - vect2))
# 或者使用内建方法
# dist = np.linalg.norm(vect1 - vect2, ord=1)
return dist
if __name__ == '__main__':
vect1 = np.array([1, 2, 3])
vect2 = np.array([4, 5, 6])
dist = get_manhattan_distance(vect1, vect2)
print(dist)
输出结果
9

