环境
- python 3.8
前言
在目标跟踪时,时常需要确定目标是否在某一区域内出现,这个问题的本质就是去判断,平面中的点是否在多边形的内部。
光线投射法
下面这张图来自维基百科,阐述了光线投射法(Ray-casting Algorithm)的基本原理
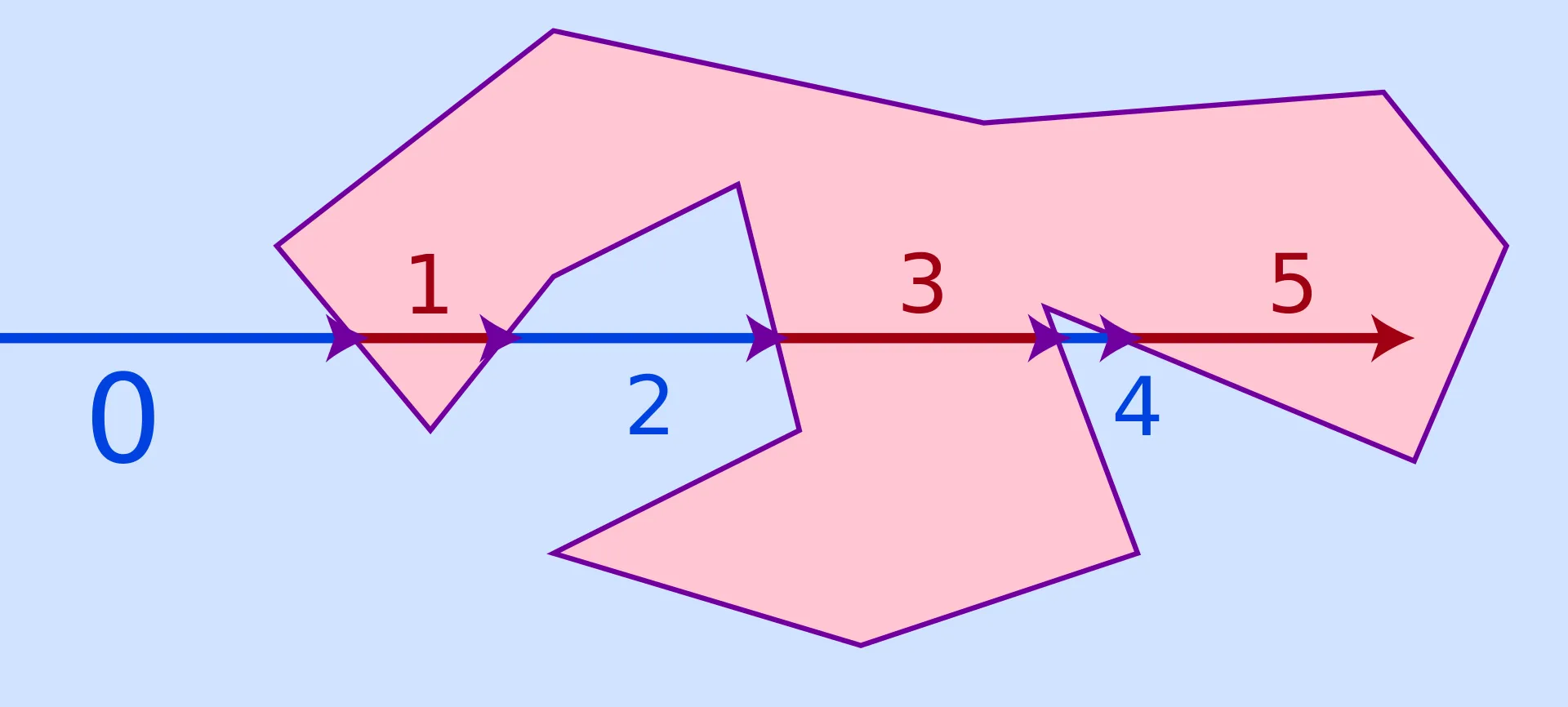
通常从待测试点出发画一条射线,可以是任意方向,然后计算直线与区域边界相交的次数,如果次数为奇数,则认为待测试点在区域内,如果是偶数,则认为待测试点在区域的外部。
代码实践
直接看代码吧
def is_in_polygon(p, polygon):
"""
:param p: [x, y]
:param polygon: [[], [], [], [], ...]
:return:
"""
px, py = p
is_in = False
# 循环处理多边形的的每一条边,判断这条边是否和以待测试点向右画出的一条设线是否相交,如有相交,则结果反转一次
for i, corner in enumerate(polygon):
next_i = i + 1 if i + 1 < len(polygon) else 0
x1, y1 = corner
x2, y2 = polygon[next_i]
# 待测试点在多边形的顶点上,返回 True
if (x1 == px and y1 == py) or (x2 == px and y2 == py):
is_in = True
break
if min(y1, y2) < py <= max(y1, y2):
# 获取相交点的 x 坐标
x = x1 + (py - y1) * (x2 - x1) / (y2 - y1)
# 在多边形的边上,返回 True
if x == px:
is_in = True
break
# 待测试点在线的左侧,结果反转一次
elif x > px:
is_in = not is_in
return is_in
if __name__ == '__main__':
point = [3, 3]
polygon = [[0, 0], [7, 3], [8, 8], [5, 5]]
print(is_in_polygon(point, polygon))



